Die Welt der Objekterkennung ist ein faszinierendes Gebiet in welches ich innerhalb einer Projektarbeit einen kurzen Einblick erhaschen konnte. Eines der Kernmetriken, um die Güte eines Objekterkennungsmodelles zu beschreiben, ist die mean Average Precision (mAP). Ich empfand es als sehr hilfreich, dass viele hilfreiche Lernresourcen in Form von Blog Beiträgen im Internet bereits vorhanden sind. Die Grundkonzepte wurden einfach und verständlich erklärt, allerdings ist die Berechnung der mAP vereinzelt sehr unterschiedlich ekrlärt worden. In diesem Beitrag möchte ich gerne meine Befunde teilen und etwas mehr Klarheit schaffen.
In diesem Beitrag wird davon ausgegangen, dass bereits grundlegendes Wissen und Verständnis der Objekterkennung angeeignet wurde, wenngleich diese auch kurz noch einmal erläutert werden. Das Ziel ist es hier eher eine bessere Intuition und erweiterte Erklärung zur Berechnung der mAP anzubieten.
Wieso die mAP?
Um eine Vergleichbarkeit von trainierten Objekterkennungsmodellen zu gewährleisten ist es wünschenswert eine Metrik zu haben, die die Güte eines einzelnen Models beschreibt. Anders als bei der Bilderkennung, ist hier nicht nur die korrekte Klassifizierung sondern auch korrekte Lokalisierung der Objekte auf dem Bild entscheidend für die Qualität des Models. Die mean Average Precision muss also her.
Ein Modeltraining erfolgt mit einem Trainingsdatensatz. Um die Qualität des trainierten Modelles zu validieren, wird es auf einen Testdatensatz angewand, welches Daten beinhaltet, die unabhängig vom Trainingsdatensatz sind. Die mAP wird dann über die Vorhersageergebnisse des Models auf dem Testdatensatz berechnet.
Intersection over Union (IoU)
Um zu bewerten, ob eine Objekterkennung erfolgreich ist, muss das Objekt vom Model richtig lokalisiert worden sein. Dazu wird die Messgröße Intersection over Union (IoU) genutzt. Sie gibt die Überlappung der Vorhersage (Prediction Box) mit der manuell gesetzten Bounding Box des Objektes (Ground Truth) an. Padilla et al., 2020[1] erklären die IoU mit einem sehr einfachem und verständlichem Graphik (siehe Bild 1, grün= ground truth, rot= bounding box).
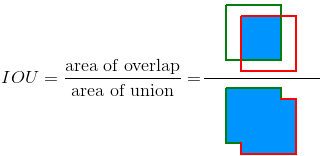
Das Ergebnis ist ein Wert zwischen 0 und 1. Je höher der Wert, desto höher die Überlappung und als bessere Vorheresage deutbar. Nun könnte man willkürlich einen Grenzwert bestimmen, ab dem eine Vorhersage als erfolgreich gilt. Für ein besseres Verständnis, gehen wir im Folgendem aus, dass wir diesen Grenzwert auf 0.5 gesetzt haben. Wenn also unsere Vorhersage zu 50% mit der Ground Truth übereinstimmt, so gilt dies als korrekte Objektdetektion.
Die IoU ist objektspezifisch und gilt als entscheidendes Kriterium, ob eine Detektion als korrekt oder nicht korrekt zählt (siehe Everingham et. al. 2010, p.11[2]). Angenommen auf einem Bild wurde eine Prediction Box für ein Objekt A vorhergesagt, an der aber eigentlich eine Ground Truth für Objekt B liegt. Auch wenn also eine Überlappung zweier Boxen stattfindet, so sind diese von zwei unterschiedlichen Objekten. Es gibt daher an dieser Stelle keine IoU für das vorhergesagte Objekt A.
Confusion Matrix – TP, FP, FN
Basierend auf dem IoU Grenzwert kann die Performance des trainierten Models nun ermittelt werden, indem die Metriken der Confusion Matrix berechnet werden.
True Positive (TP): Der IoU > Grenzwert.
- Eine Vorhersage wurde getätigt, dessen Überlappung mit der Ground Truth des vorhergesagten Objektes größer als unser festgelegter Grenzwert ist.
False Positive (FP): Der IoU < Grenzwert.
- Unser Model hat eine Prediction Box vorhergesagt, welches nicht gut genug mit der Ground Truth überlappt
- ODER die Prediction Box ist gut gewählt, jedoch ist die darunterliegende Klasse der Ground Truth eine andere. Somit ist die IoU nicht existent, weil es keine Überlappung von Prediction Box und Ground Truth des spezifischen Objektes gibt. (Dies könnte man auch als Fall einer Misklassifikation ansehen)
- Wenn ein Objekt mehrere Male detektiert wurde, dann wird nur die Prediction Box mit der höchsten Konfidenz (nicht der IoU) als TP gewählt, alle anderen Vorhersagen werden zu den FP gezählt (siehe Everingham et. al. 2010, p.12 [2] ).
False Negative (FN): Eine Ground Truth wurde gar nicht detektiert, obwohl das Objekt im Bild vorkommt
True Negative (TN): Ist nicht relevant, da diese Metrik nur die richtige Vorhersage von nicht gewählten Prediction Boxen beinhaltet.
- Wenn beispielsweise auf einer freien Fläche keine Prediction Box gelegt wurde und diese auch keine Objekte und daher keine Ground Truth besitzt wäre das eine erfolgreiche Vorhersage einer nicht existenten Ground Truth (TN). Da wir jedoch nur die korrekten Vorhersagen die auch ein Objekt beinhalten betrachten wollen, ist diese Metrik für uns nicht relevant
Mit Hilfe der TP, FP und FN lassen sich bekannte Metriken aus der Confusion Matrix berechnen:
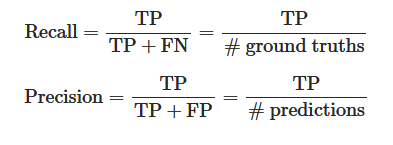
Eine hohe Precision deutete darauf hin, dass viele Vorhersagen korrekt getroffen wurden (daher niedrige FP). Ein hoher Recall Wert impliziert, dass die meisten Objekte gefunden wurden (daher niedrige FN). Die Beziehung von Precision und Recall kann in einer Precision-Recall Kurve visuell gezeigt werden.
Die Precision-Recall Kurve
An dieser Stelle möchte ich gerne auf Padilla et al., 2020[1] ‘s git repository verweisen, wo sie sehr schön die Berechnung der Precision-Recall Kurve an einem umfassendem Beispiel illustrieren. Im Folgendem wird ihre Arbeit nur kurz zusammengefasst mit vereinzelt erweiterten Erklärungen. Auch Interpolation wird im Orginal Paper der Pascal VOC Challenge erwähnt, aber hier außen vor gelassen ( siehe Everingham et. al. 2010, p.11[2]).
Für jede Vorhersage erhalten wir einen Konfidenzwert und basierend auf den IoU ob es ein TP oder FP ist. Wir sortieren alle Ergebnisse nach Konfidenzwerten in absteigender Reihenfolge und kumulieren die Anzahl der TP und FP. Unter Nutzung der kumulierten TP und FP werden nun die Precision und Recall-Werte für jede Vorhersage in der entsprechenden Reihenfolge berechnet. Das Ergebnis lässt sich in einer Precision-Recall Kurve darstellen
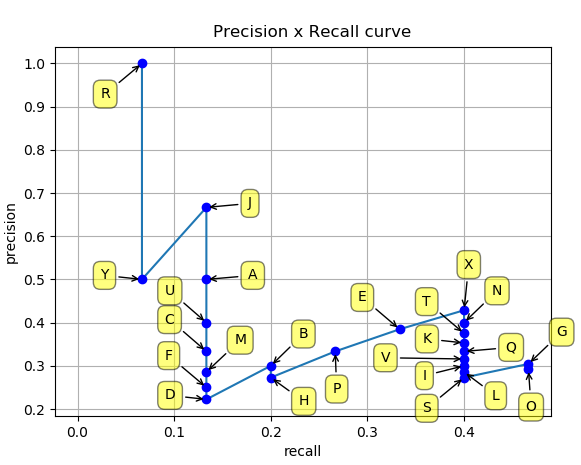
Es liegt in der Natur der Kurve, dass die Precision am Anfang hoch ist, da noch wenige Fehlerkennungen vorliegen (niedrige FP). Viele Objekte wurden jedoch noch nicht erkannt (hohe FN), was zu einem niedrigem Recall Wert führt. Mit zunehmender Betrachtung weiterer Vorhersagen steigt der Recall, da mehr und mehr Objekte erkannt werden (sinkende FN), jedoch auch zunehmend mehr Fehlerkennungen (steigende FP) auftreten, was zu einer Verringerung der Precision führt.
Eine Objekterkennung gilt als gut, wenn sie mit steigendem Recall trotzdem noch einen hohen Precision Wert aufweisen kann. Dies würde bedeuten, dass sowohl ein großer Teil der Objekte erkannt wurden (geringe FN), ohne zu viele fehlerhafte Vorhersagen getätigt zu haben (geringe FP).
Die Average Precision
Durch die eingeführte Precision-Recall Kurve lassen sich verschiedene Testergebnisse miteinander vergleichen. Statt jedoch diese Graphen gegenüberzustellen, wäre es hilfreich, eine einzelne numerische Zahl abzuleiten, an Hand derer der Vergleich stattfinden kann. Die durchschnittliche Precision (Average Precision (AP)) über alle Recall Werten zwischen 0 und 1 kann hier als Performanceindikator für den Klassifikator genutzt werden und entspricht der Fläche unter der Precision-Recall Kurve. Da die Kurve geprägt von zick-zack Linien ist, gibt es verschiedene Herangehensweisen diese Fläche (=AP) zu approximieren. An dieser Stelle möchte ich wieder an Padilla et al., 2020[1] und EL Aidouni, 2019[3] verweisen, die auf sehr anschaulicher Art zeigen, wie die Interpolation durchgeführt wird. Die Interpolation kann von Wettbewerb zu Wettbewerb unterschiedlich sein und hat minimalen aber dennoch signifikanten Einfluss auf das resultierende Ergebnis.
Für die Pascal VOC Challenge:
- Vor 2010 wurde eine 11-Punkte Interpolation genutzt (siehe Everingham et. al. 2010, p.11[2])
- nach 2010 wird jeder Punkt für die Interpolation genutzt
Für die COCO Challenge:
- Eine 101- Punkte Interpolation wird genutzt ( siehe cocodataset.org Sektion 3, “recThrs”)
Die mAP
Zu beachten ist, dass die bisherige Berechnung der AP über die Precision-Recall Kurve nur eine Klasse betrifft, wohingegen in der Objekterkennung typischerweise mehrere Klassen auftauchen. Eine gesamtheitliche Metrik um die Performance des Models zu ermitteln ist daher die Mean Average Precision (mAP), welche den Durchschnitt der AP über alle Klassen hinweg bildet.
Weiterhin ist die Berechnung der Precision-Recall Kurve (und somit der mAP) abhängig davon, wann eine Objekterkennung als richtig eingestuft wird, welche wiederrum von dem IoU-Grenzwert abhängig ist. Unterschiedliche IoU-Grenzwerte erzeugen unterschiedliche Precision-Recall Kurven. Auch hier haben unterschiedliche Wettbewerbe die Berechnung der mAP unterschiedlich definiert.
Für die Pascal VOC Challenge wird ein einziger IoU Grenzwert von > 0.5 definiert, aus dem die mAP berechnet wird (see Everingham et. al. 2010, p.11[2]).
Für die COCO Challenge erfolgt die Ermittlung der primären mAP über den Durchschnitt aller AP für jeweils einen IoU zwischen 0.5 und 0.95 mit einer Schrittzahl von 0.05. Die mAP Berechnung mit einem einzelnem IoU Grenzwert von 0.5 wurde weiterhin beibehalten und als [email protected] benannt sowie weitere spezielle Metriken eingeführt ( siehe cocodataset.org Sektion 2).
Randnotiz:
In Harshit Kumar’s Blog Eintrag wird bereits erwähnt, dass die Art und Weise, wie die Pascal VOC Challenge die mAP berechnet, den Nachteil hat, dass den einzelnen Ergebnissen keine Gewichtung zugeteilt wird. Ein Ergebnis mit einer IoU von 0.6 wird gleich gewertet wie ein Ergebnis mit einer IoU von 0.9. Diesen Gedanken wollen wir hier forführen. In Tabelle 1 und 2 können wir vier Detektionen erkennen.
| Detektion | IoU |
| 1 | 0.9 |
| 2 | 0.6 |
| 3 | 0.6 |
| 4 | 0.6 |
| Detektion | IoU |
| 1 | 0.9 |
| 2 | 0.9 |
| 3 | 0.9 |
| 4 | 0.6 |
Als vereinfachtes Beispiel soll angenommen werden, dass nur ein Objekt A erkannt werden soll. Der IoU Grenzwert wurde auf 0.5 fest gesetzt und es gibt nur vier Objekte die, wie in Tabelle 1 und 2 zu sehen, alle erkannt worden (TP = 4), sodass es keine FN gibt. Nach der Pascal VOC Challenge ist somit die mAP für beide Detektionen in Tabelle 1 und 2 gleich (mAP = 1, alles erkannt), allerdings kann klar erkannt werden, dass die Detektion in Tabelle 2 die Objekte insgesamt besser lokalisieren konnte.
Wie können also bessere Lokalisierungen auch höher gewichtet werden? Die COCO Challenge versucht diesen Umstand entgegenzusteuern, indem sie für verschiedene IoU Grenzwerte die AP berechnet und dessen Durchschnitt berechnet. Die definierten IoU Grenzwerte sind von 0.5 bis 0.95 mit einer Schrittgröße von 0.05 ( siehe cocodataset.org Sektion 2, 1.). Wir können diese Idee an unserem Beispiel demonstrieren, indem wir vereinfacht zwei Grenzwerte bei 0.5 und 0.75 einfügen.
Die AP für einen IoU Grenzwert von 0.5 ist für beide Messungen immer noch 1. Allerdings wird sich die AP für einen IoU Grenzwert von 0.75 zwischen den beiden Messungen unterscheiden:
| Detektion | IoU | TP | FP | acc TP | acc FP | Precision | Recall |
| 1 | 0.9 | 1 | 0 | 1 | 0 | 1/(1+0) = 1 | 1/(1+3) = 0.25 |
| 2 | 0.6 | 0 | 1 | 1 | 1 | 1/(1+1) = 0.5 | 1/(1+3) = 0.25 |
| 3 | 0.6 | 0 | 1 | 1 | 2 | 1/(1+2) = 0.33 | 1/(1+3) = 0.25 |
| 4 | 0.6 | 0 | 1 | 1 | 3 | 1/(1+3) = 0.25 | 1/(1+3) = 0.25 |
| Detektion | IoU | TP | FP | acc TP | acc FP | Precision | Recall |
| 1 | 0.9 | 1 | 0 | 1 | 0 | 1/(1+0) = 1 | 1/(1+1) = 0.5 |
| 2 | 0.9 | 1 | 0 | 2 | 0 | 2/(2+0) = 1 | 2/(2+1) = 0.66 |
| 3 | 0.9 | 1 | 0 | 3 | 0 | 3/(3+0) = 1 | 3/(3+1) = 0.75 |
| 4 | 0.6 | 0 | 1 | 1 | 1 | 3/(3+1) = 0.75 | 3/(3+1) = 0.75 |
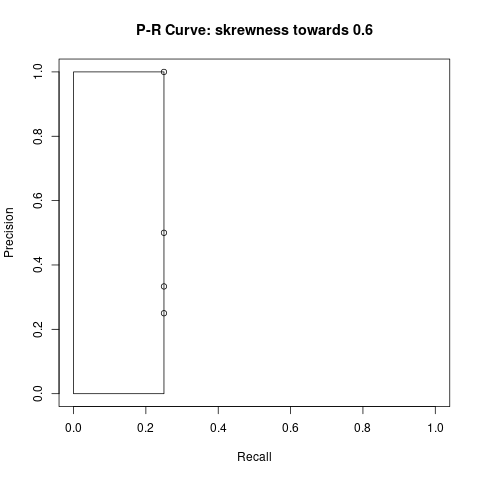
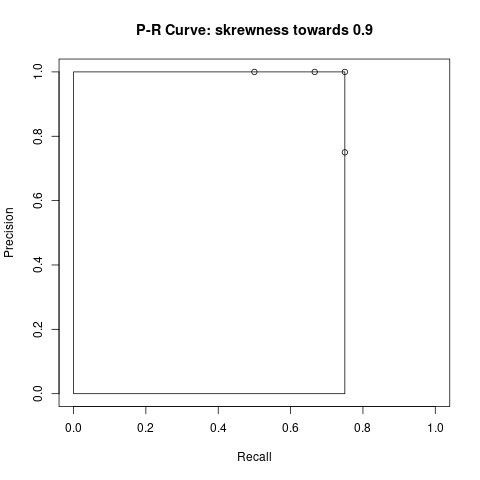
In Tabelle 3 kann beobachtet werden, dass die Detektionen 2 bis 4 den IoU Grenzwert nicht überschreiten und somit als FP gezählt werden. Dadurch, dass diese Objekte nicht gefunden wurden, erhöht sich auch der FN auf 3. Die Precision und Recall Werte werden stets mit den kumulierten TP und FP Werten berechnet. Die mAP ist die Fläche (Rechteck) unter der Kurve, die wir in Bild 4 und 5 sehen können.
Die finale Berechnung der mAP für die Beispiele aus Tabelle 1 und 2 ist wie folgt:
Tabelle 1: Beispiel mit erhöhter Detektion bei IoU = 0.6
- [email protected] = 1
- [email protected] = 0.25*1 = 0.25
- average mAP = (1 + 0.25) / 2 = 0.625
Tabelle 2: Beispiel mit erhöhter Detektion bei IoU = 0.9
- [email protected] = 1
- [email protected] = 0.75 * 1 = 0.75
- average mAP = (1 + 0.75) / 2 = 0.875
Wie zu erwarten erhalten wir nun ein differenzierteres Ergebnis. Das Beispiel aus Tabelle 2 mit überwiegend hoher Lokalisierungsgenauigkeit hat im Vergleich auch einen höheren mAP Wert.
Weiterführende Links
Wie bereits erwähnt, ist eine sehr gute und umfassende Resource das git Repository von R. Padilla et. al. : https://github.com/rafaelpadilla/Object-Detection-Metrics. Mir hat jedoch ein bisschen die Intuition gefehlt und auch die Differenzierung zwischen den beiden Wettbewerben und ihren EInfluss auf die Berechnung der Metriken, was der Hauptgrund für diesen Blog Eintrag ist.
Manal El Aidouni stellt sehr schöne visuelle Darstellungen bereit und bietet ein erweitertes intuitives Verständnis für die Metriken. Ein kleines Manko: Sein Absatz “Precision – recall and the confidence threshold” sollte wohl mehr als zusätzliche Randnotiz verstanden werden, als wirklich zur Berechnung der mAP beitragen: https://manalelaidouni.github.io/manalelaidouni.github.io/Evaluating-Object-Detection-Models-Guide-to-Performance-Metrics.html
Harshit Kumar gibt einen sehr verdichteten Überblick über das Thema der Berechnung der mAP und ist doch sehr einfach zu lesen, wenn man sich mit dem Thema schon auseinander gesetzt hat: https://kharshit.github.io/blog/2019/09/20/evaluation-metrics-for-object-detection-and-segmentation
Jonathan Hui’s gibt in seinem Blog Beitrag auch eine sehr gute Zusammenfassung, welche ich jedoch nicht als Resource genutzt habe, der Vollständigkeit halber aber gerne mit auflisten möchte: https://jonathan-hui.medium.com/map-mean-average-precision-for-object-detection-45c121a31173
Referenzen
- Padilla, R., S. L. Netto, E. A. B. da Silva (2020). „A Survey on Performance Metrics for Object-Detection Algorithms“. In: 2020 International Conference on Systems, Signals and Image Processing (IWSSIP), p. 237–242. | git repository [↩][↩][↩][↩][↩]
- „The Pascal Visual Object Classes (VOC) Challenge“. In: International Journal of Computer Vision 88.2, S. 303–338. issn: 0920-5691, 1573-1405. doi:10.1007/s11263-009-0275-4. url: http://link.springer.com/10.1007/s11263-009-0275-4 (last visit 22. 11. 2020).[↩][↩][↩][↩][↩]
- EL Aidouni, Manal (5. Okt. 2019). Evaluating Object Detection Models: Guide to Performance Metrics. url: https://manalelaidouni.github.io/manalelaidouni.github.io/Evaluating-Object-Detection-Models-Guide-to-Performance-Metrics.html#average-precision (visitedam 05. 11. 2020). [↩]
nice